ノルウェーメンサの回答・解説

ノルウェーメンサの公開テストが更新されました。

こちらのページは過去問題での解説ですので最新版は下記リンクよりご覧ください。

前回、ノルウェーメンサの問題について触れましたが、今回はノルウェーメンサ問題の回答や解き方について説明したいと思います。

ノルウェーと言っても、言葉の問題はでないから一度試しにやってみてください。この先は回答になるので、先にやっておいた方が良いです。

どうでしたか？

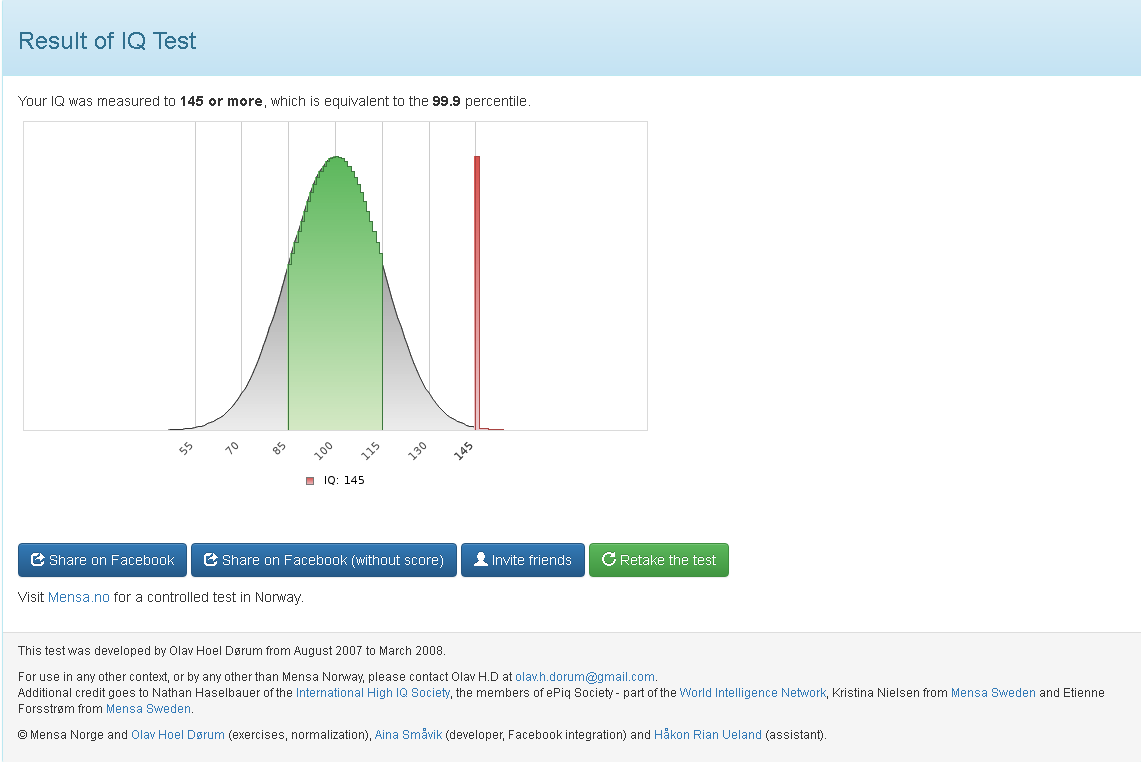
私は、最初130程度、2回目は145となりました。最高が145なので最高ですね。2回目は推理し答えがある程度わかったので上がって当然なので・・・。

Exercise 1

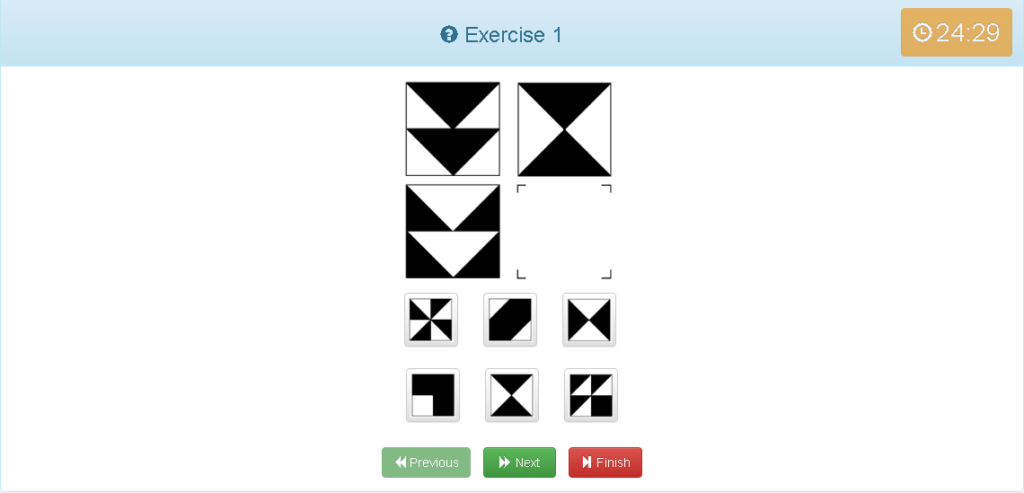
解説

1. 縦でグルーピング。
2. 黒が白、白が黒に変わっている。
3. 図形は同じ

答え

Exercise 2

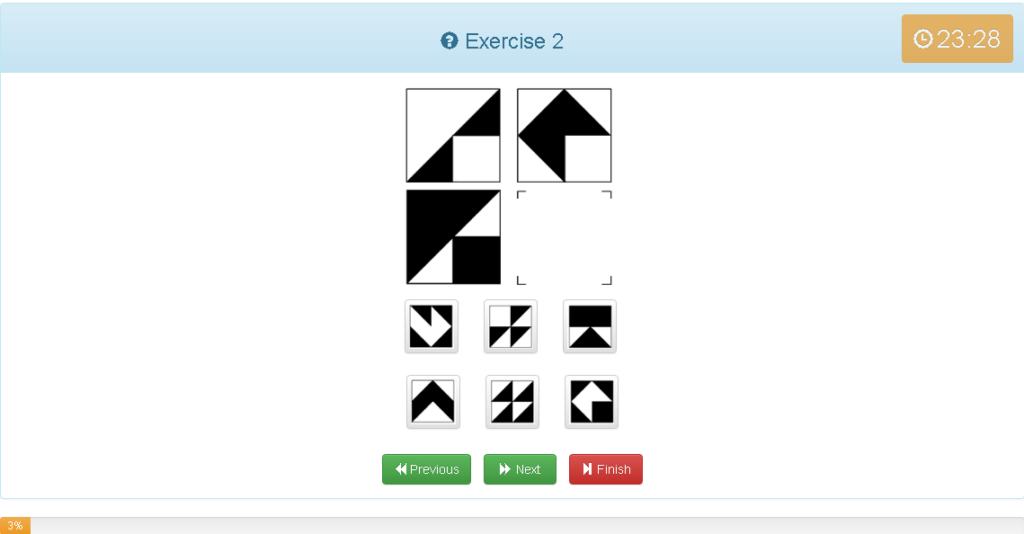
解説

1. 縦でグルーピング。
2. 黒が白、白が黒に変わっている
3. 図形は同じ

答え

Exercise 3

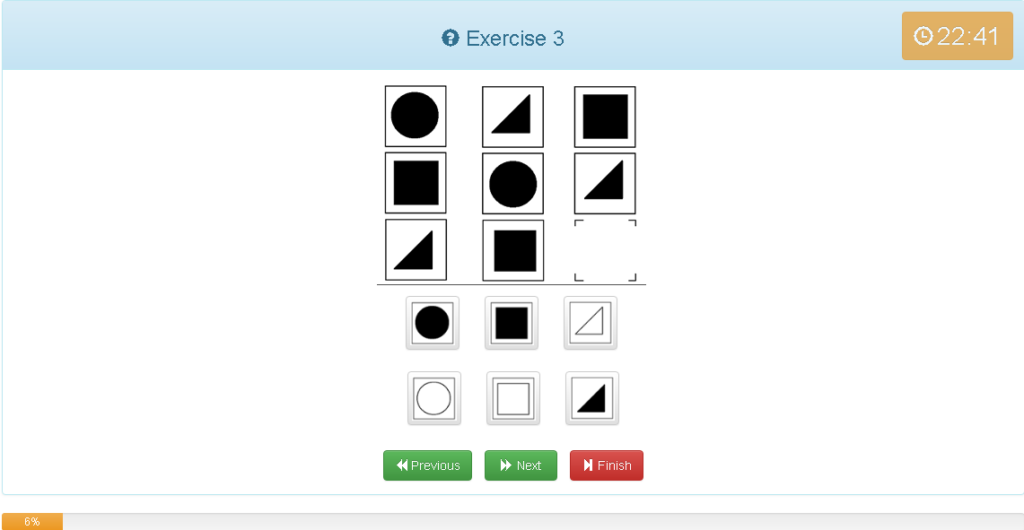
解説

1. 縦でも横でもグルーピングできる
2. ●を基準とする
3. 縦は●・■・▲の順で上から並んでいる
4. 横は●・▲・■の順で左から並んでいる
5. それが1マスずつズレている
6. 図形は同じ
7. 他の考え方として、9マス中3マス埋まっていないのは●だけである

答え

Exercise 4

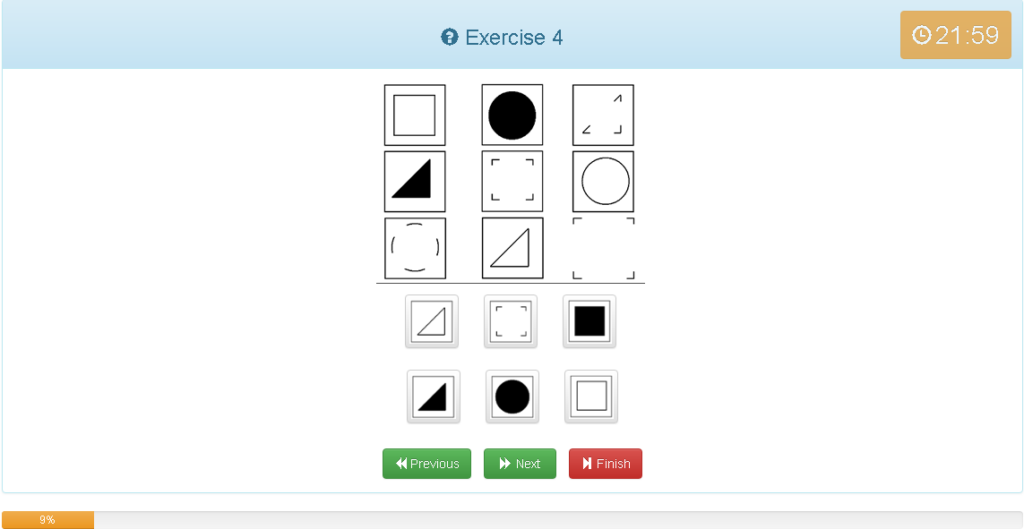
解説

1. 縦横どちらでもグルーピングできる
2. 縦では左上の□を基準に□・▲・点〇の順
3. 横では左上の□を基準に□・●・点△の順
4. それぞれが1マスずつズレている
5. 図形は同じ
6. 他の考え方として9マス中3マス埋めていないのは□、そのうち塗りつぶしが無いのは四角のみ
7. 法則が分かれば斜めに見ると早い

答え

Exercise 5

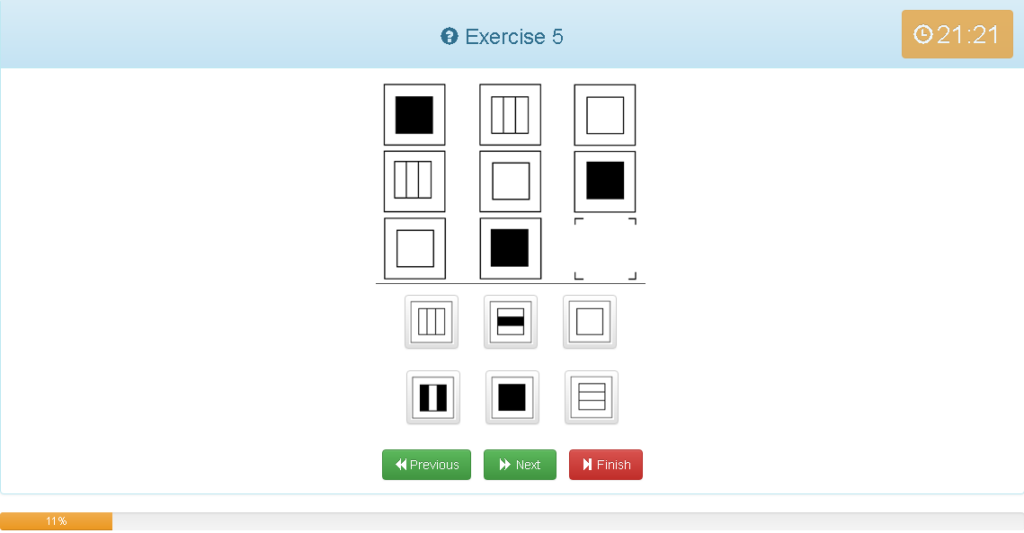
解説

1. 縦横どちらでもグルーピングできる
2. 縦でも横でも左上の■を基準に■・しま・□の順
3. それぞれが1マスずつズレている
4. 図形は同じ
5. 他の考え方として9マス中3マス埋めていないのはしま模様、そのうち塗りつぶしが無いのは四角のみ
6. 法則が分かれば斜めに見ると早い

答え

Exercise 6

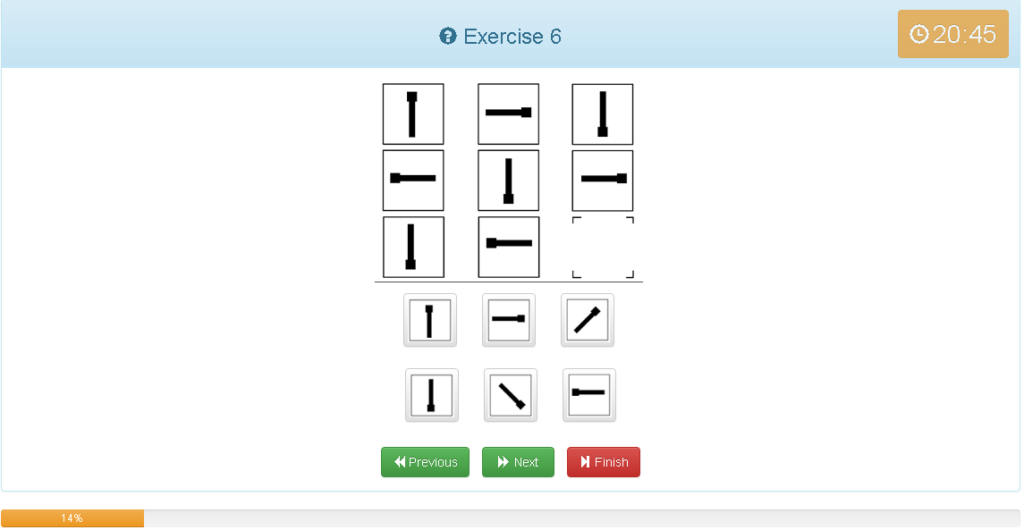
解説

1. 縦でも横でもグルーピングできる
2. 縦では反時計回りに回転している
3. 横では時計回りに回転している
4. 他の考え方では、1マス90度の回転であれば斜めでは2マスなので180度の回転となる、よって法則が分かれば左上の画像と同じになるのが予想できる。

答え

Exercise 7

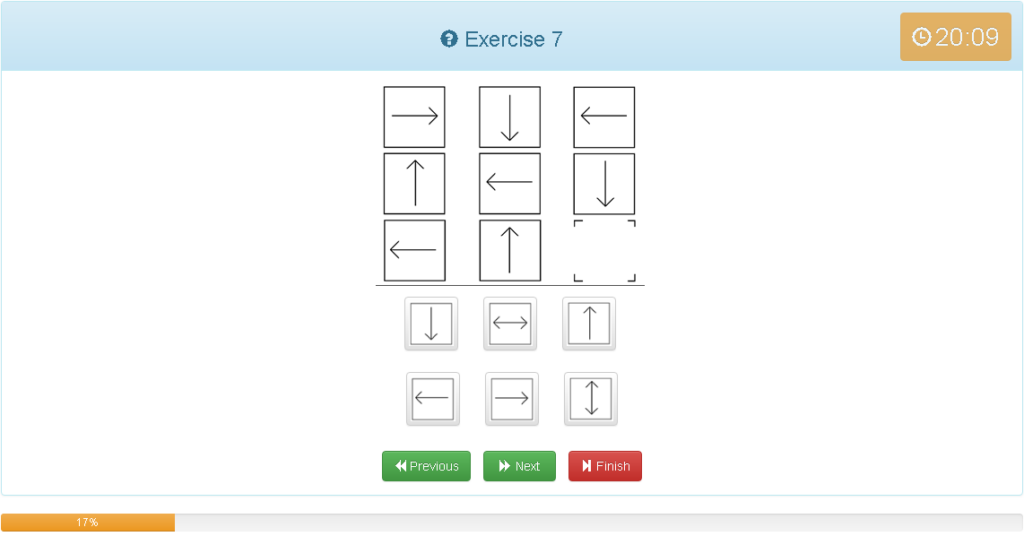
解説

1. 縦でも横でもグルーピングできる
2. 縦では時計回りに回転している
3. 横では反時計回りに回転している
4. 他の考え方では、1マス90度の回転であれば斜めでは2マスなので180度の回転となる、よって法則が分かれば左上の画像と同じになるのが予想できる。

答え

Exercise 8

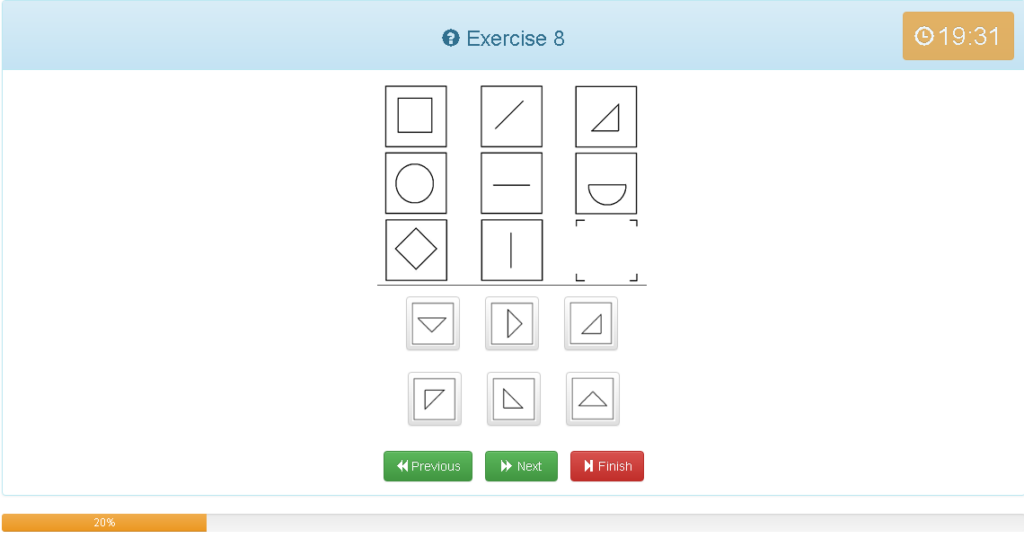
解説

1. 縦でグルーピング
2. 縦2列目の線を縦1列目の図形に合わせる
3. できた図形から半分取り除いた図形が3列目
4. 回答の中には縦線で区切られた図形は一つしかないので予想できる

答え

Exercise 9

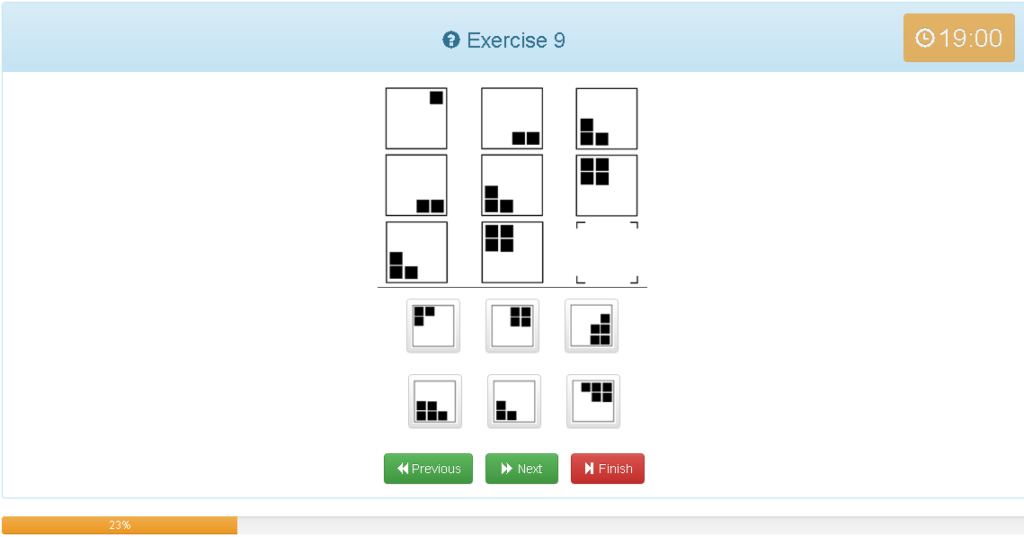
解説

1. 縦横どちらでもグルーピングできる
2. 時計回りに■が一つずつ増えている
3. 回答マスの1マス前が4個の左上にある為、次は右上の5個である
4. 他の考え方では、1マス90度の回転であれば斜めでは2マスなので180度の回転となる、よって法則が分かれば左上の画像と同じ位置で4個足した数字が予想できる。

答え

Exercise 10

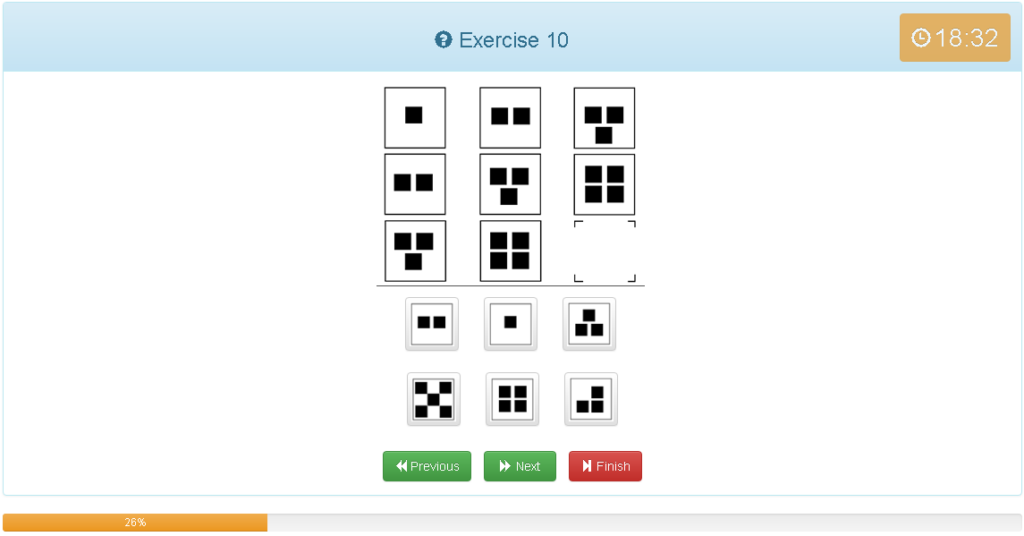
解説

1. 縦横どちらでもグルーピングできる
2. ■が一つずつ増えている
3. 回答マスの1マス前が4個の為、次は5個である
4. 他の考え方では、1マス1個であれば斜めでは2マスなので2個を斜めに足せば5になる、よって法則が分かれば左上の画像と同じ位置で4個足した数字が予想できる。

答え

Exercise 11

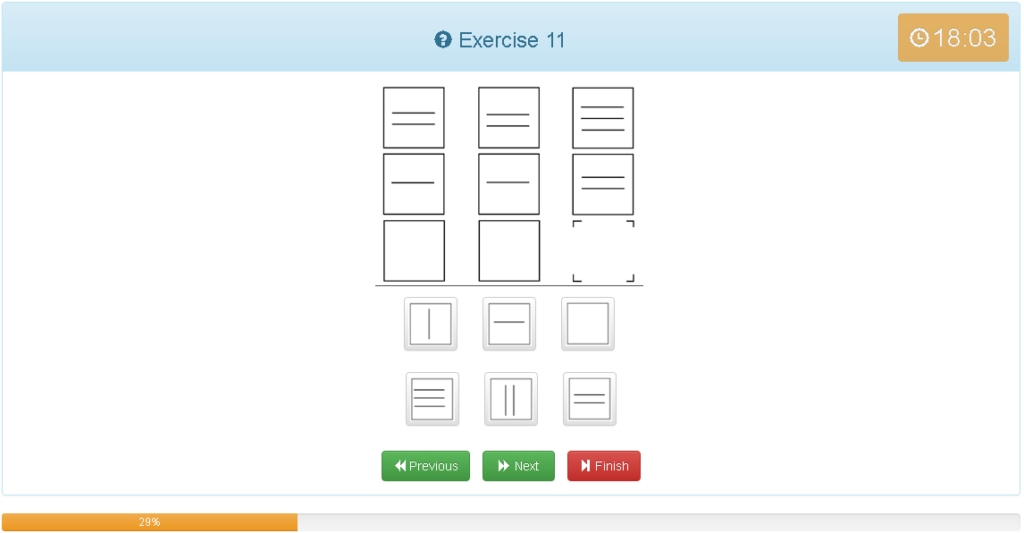
解説

1. 縦でグルーピング
2. 線が1本ずつ少なくなっている
3. 線の向きは同じ

答え

Exercise 12

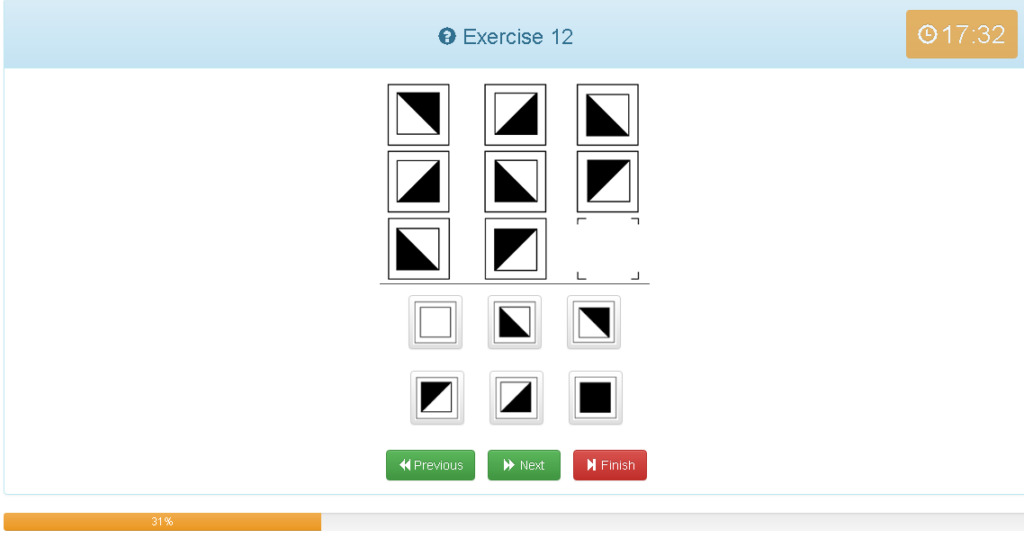
解説

1. 縦横どちらでもグルーピングできる
2. 左上の図形を基準とし反時計回りで回転している
3. 他の考え方では、1マス90度の回転であれば斜めでは2マスなので180度の回転となる、よって法則が分かれば左上の画像と同じになるのが予想できる。
4. また、右上から斜めに見ると図形がそろっていることが確認できる。

答え

Exercise 13

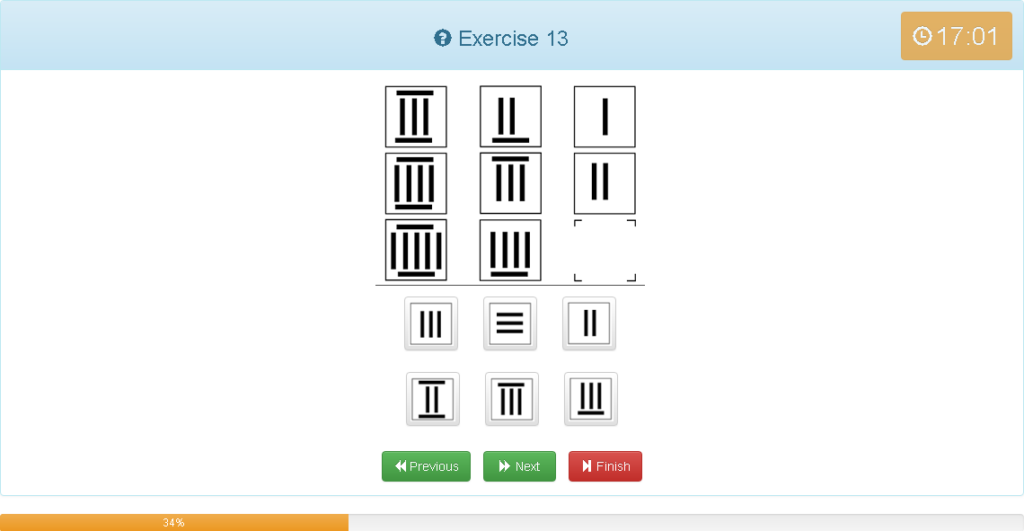
解説

1. 横でグルーピング
2. 右に行くにつれ、横線1本縦線1本が減っている
3. 線の向きは同じ

答え

Exercise 14

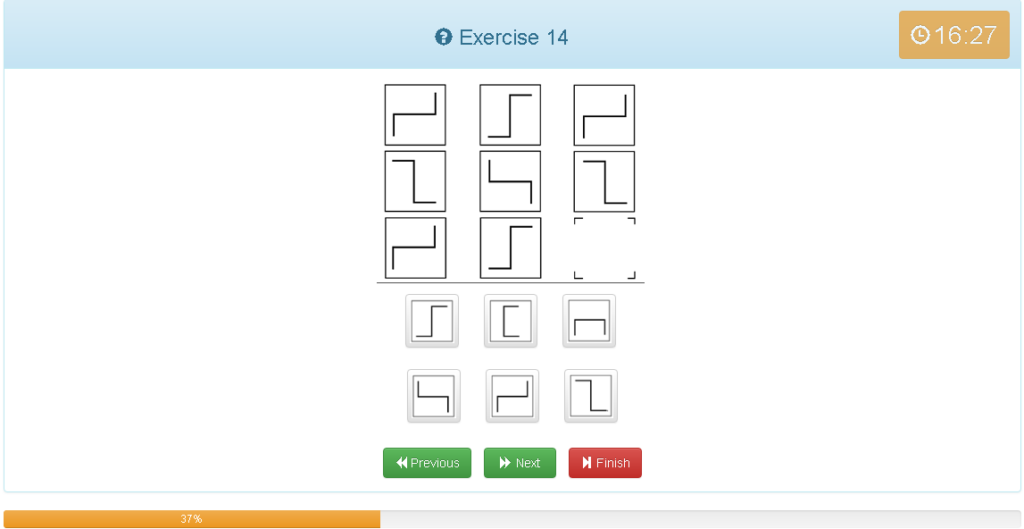
解説

1. 縦でグルーピング
2. 反時計回りに90度ずつ回転している
3. 横で考えた場合、図形の中心で割り180度回転させる（図形を法則通りに反時計回りに回転し、それを裏側から見た図形。この考え方は難しいのです。）

答え

Exercise 15

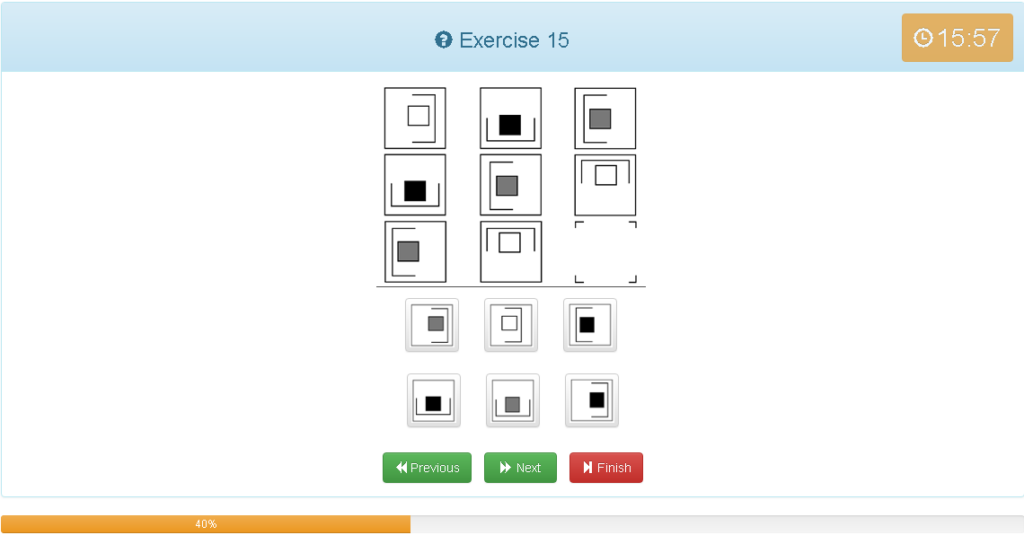
解説

1. 縦横どちらでもグルーピングできる
2. 外側の括弧が時計回りで90度回転している
3. 内の四角が、白・黒・グレーの順で変わっている
4. 右上から斜めに見ると法則が分かりやすい

答え

Exercise 16

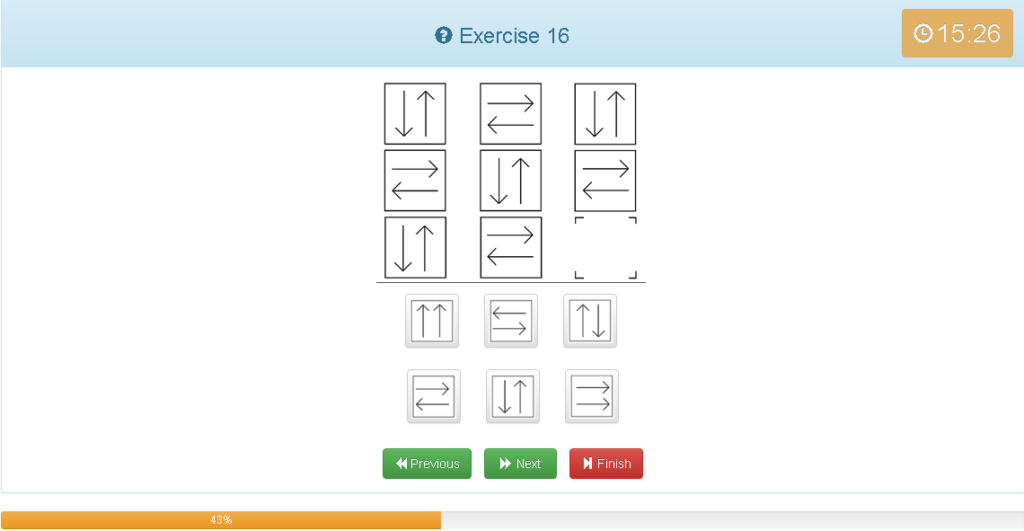
解説

1. 横でグルーピング
2. 斜めに折り線を入れるイメージ
3. それを逆に開く（90度回転して裏側から見るイメージ）
4. もっとわかりやす方法は図形は2種類しかない
5. 斜めで見ると同じ図形が並んでいる

答え

Exercise 17

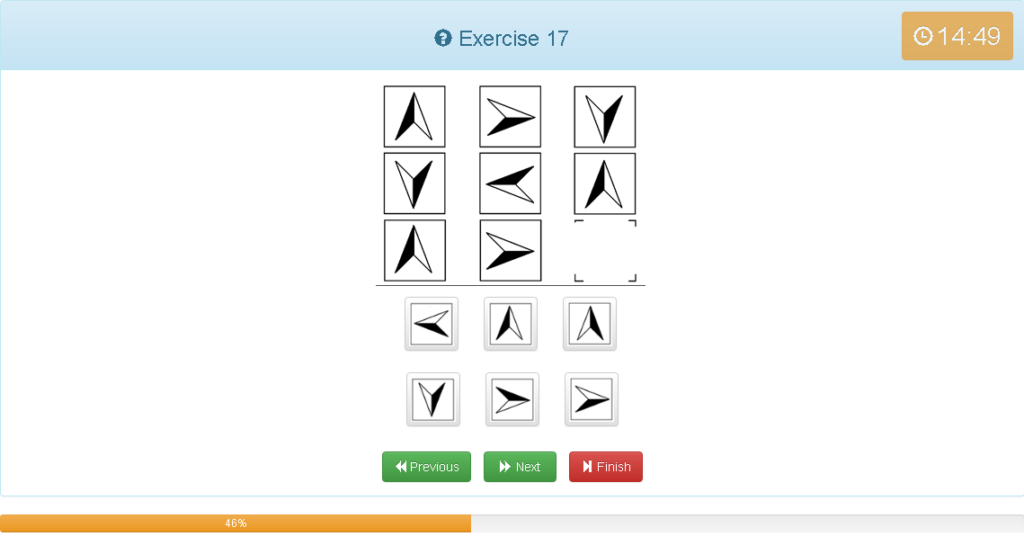
解説

1. 縦でグルーピング
2. 180度回転している
3. 180度回転しているので右上の図形と同じになる
4. 他の考え方は、横のグルーピングで90度回転し反転（裏返し）←難しい

答え

Exercise 18

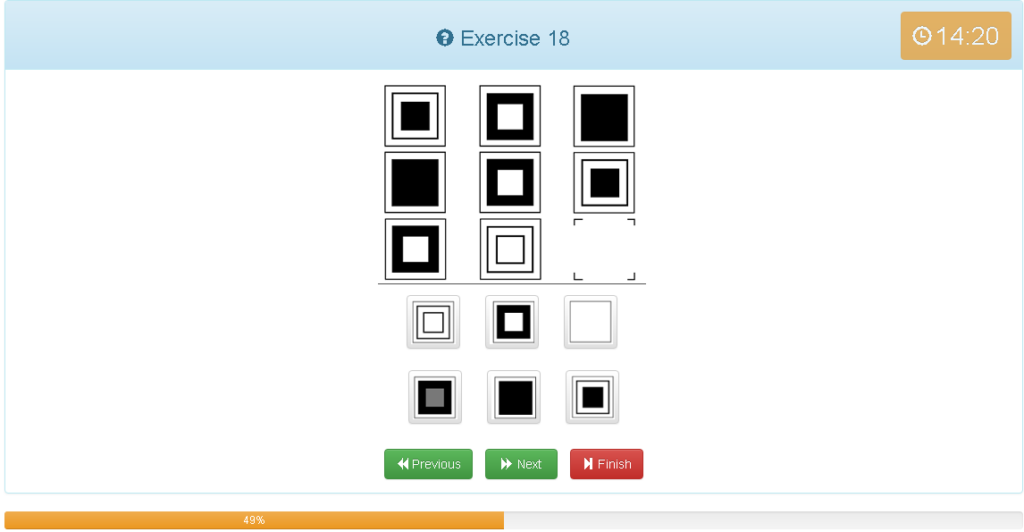
解説

1. 縦横どちらでもグルーピングできる
2. 白＋白＝白
3. 黒＋黒＝白
4. 白＋黒＝黒
5. この法則は縦横のみ斜めでは使えない（使えるがややこしい）

答え

Exercise 19

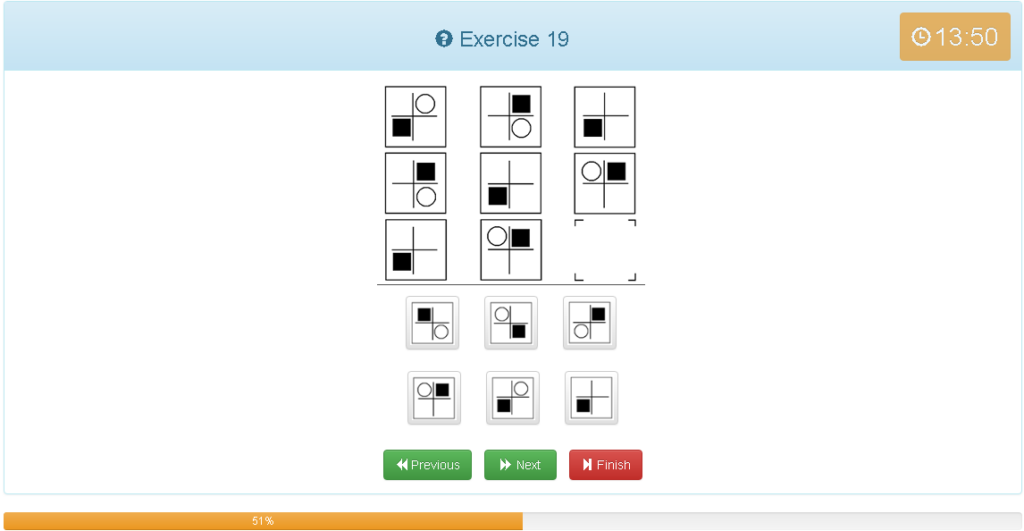
解説

1. 縦横どちらでもグルーピングできる
2. 〇が時計回りに90度回転
3. ■が180度回転（移動）
4. 他に、左上から斜めで見ると■は1マス180度なので斜めでは2マスとなり360度で位置が動きません。〇は1マス90度で斜めでは2マスとなり180度で左上の図形と同じになります。

答え

Exercise 20

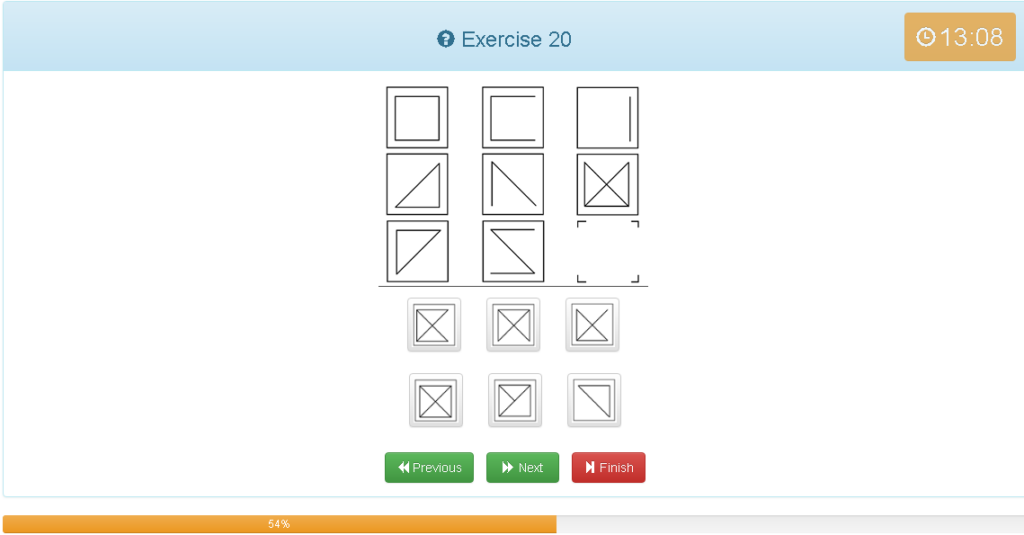
解説

1. 縦横どちらでもグルーピングできる
2. 縦で解説すると、左上の図形から2つ目の図形の線を足す。重複した線は消す。
3. この問題は横で考えるより縦で考えた方が早いです。右上の図形が線一本なので。

答え

Exercise 21

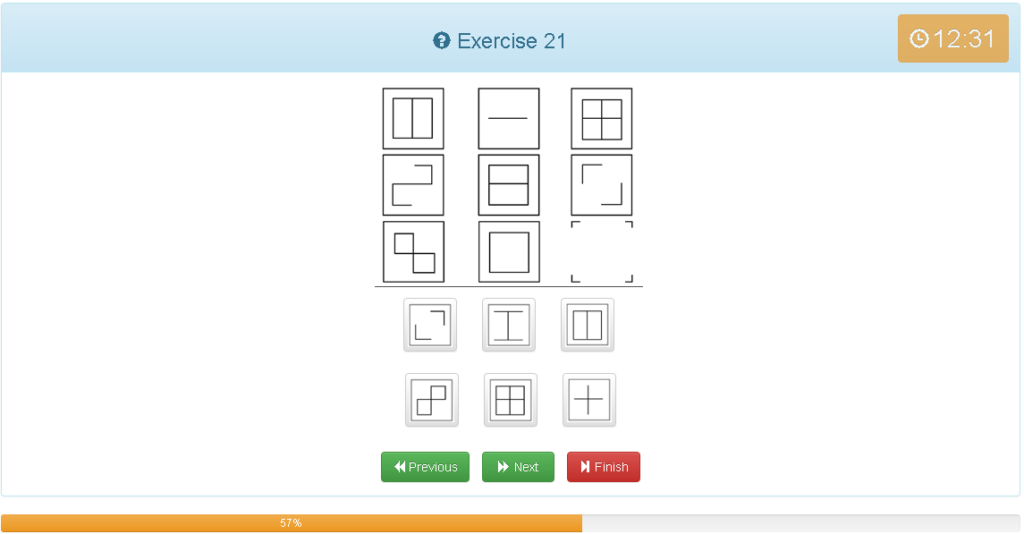
解説

1. 縦横でグルーピングできる
2. 右上の図形に2つ目の図形を足します。重複した線は消す。
3. 20の問題と同じ考え方です。

答え

Exercise 22

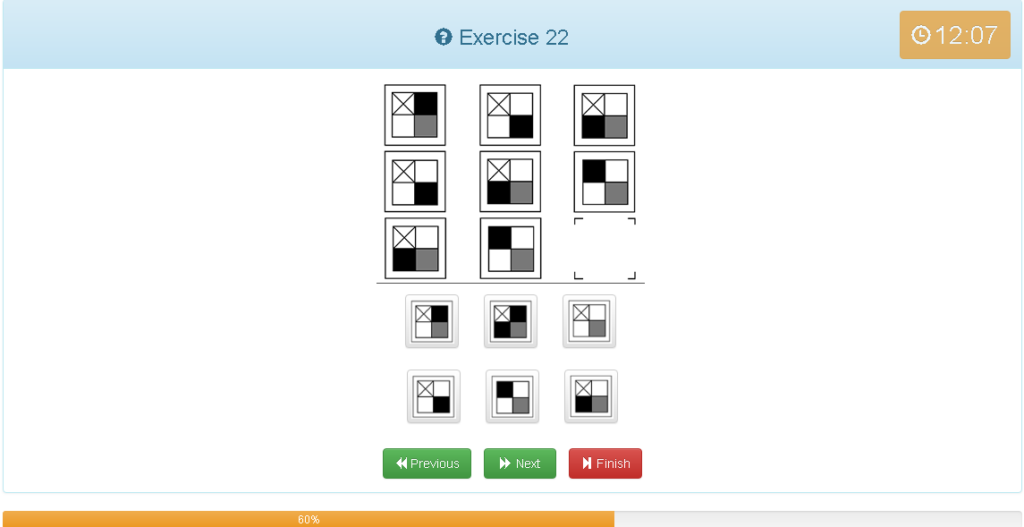
解説

1. 縦横どちらでもグルーピングできる
2. ■以外の位置は固定と考えます。
3. ■は時計回りに90度回転しています。
4. ■が1番強いと思ってください（黒が重なれば黒になる）
5. 他の考え方では、1マス90度の回転であれば斜めでは2マスなので180度の回転となる、よって法則が分かれば左上の画像と同じになるのが予想できる。

答え

Exercise 23

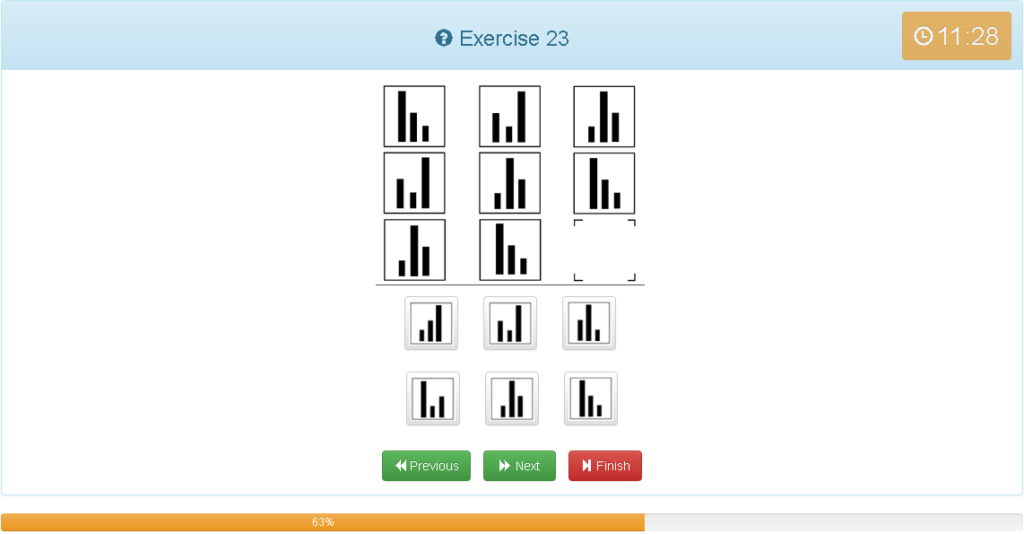
解説

1. 縦横どちらでもグルーピングできる
2. 長・中・短の線が一つずつズレている
3. 左へズレるイメージ
4. 他の考え方をすると、1マスで左へ1つズレるので斜めで考えると2マスずれることになります。3本線で2マスずれると右へ1つズレていくことが予想できます。

答え

Exercise 24

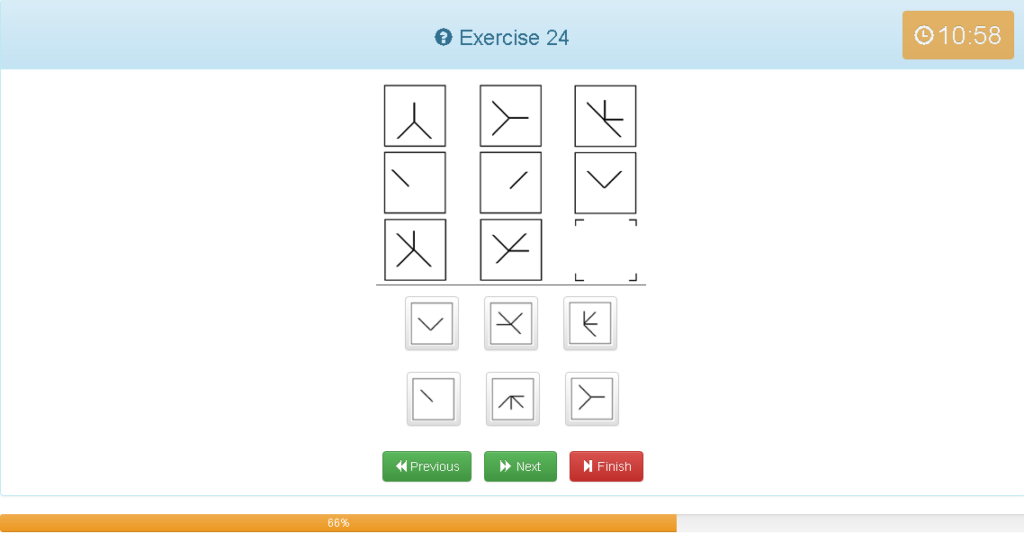
解説

1. 縦横どちらでもグルーピングできる
2. 左上の図形に2つ目の図形を足します。
3. 重複した線は消す。

答え

Exercise 25

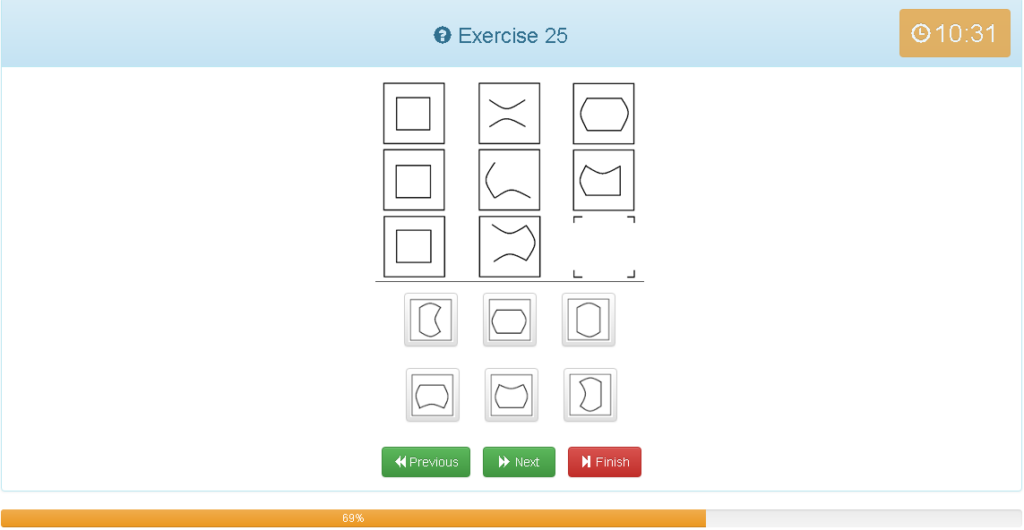
解説

1. 横でグルーピング
2. 2つ目の図形を時計回りに90度回転させ、凹凸を逆にします。
3. 1つ目の図形に2つ目の図形の返還した部分を置き換えます。

答え

Exercise 26

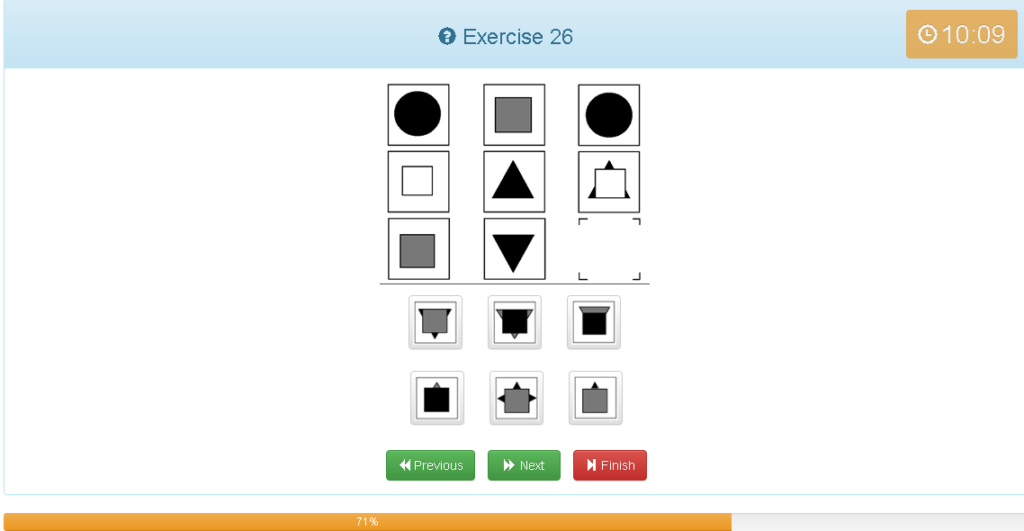
解説

1. 横でグルーピング
2. 1つ目と2つ目を足します。
3. 左側の図形が上にくるようにする

答え

Exercise 27

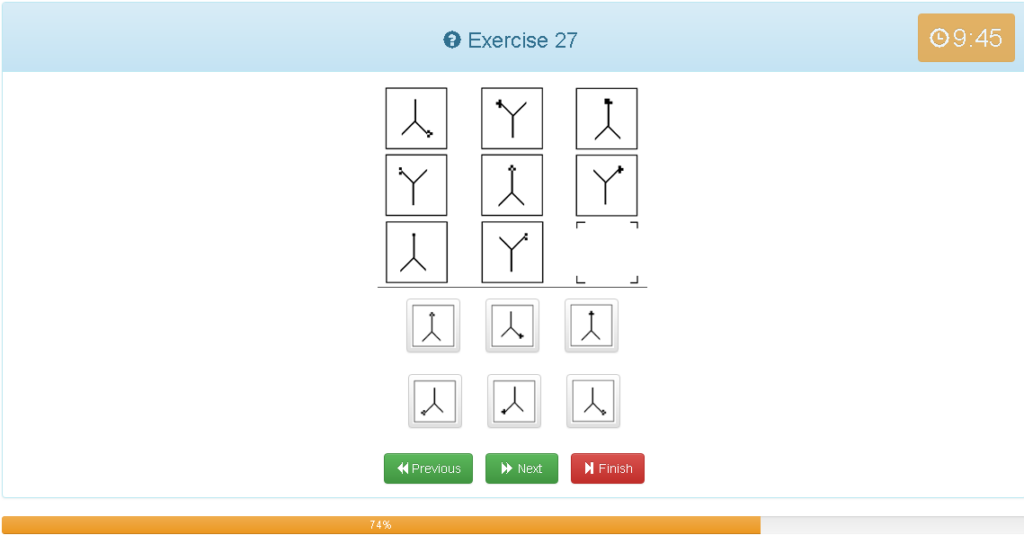
解説

1. 縦横どちらでもグルーピングできる
2. Yが180度回転していて、右に行くにつれ●の数が１つずつ増えています。下に行くにつれ１つずつ減っています。
3. Yの先端それぞれに●が移動している

答え

Exercise 28

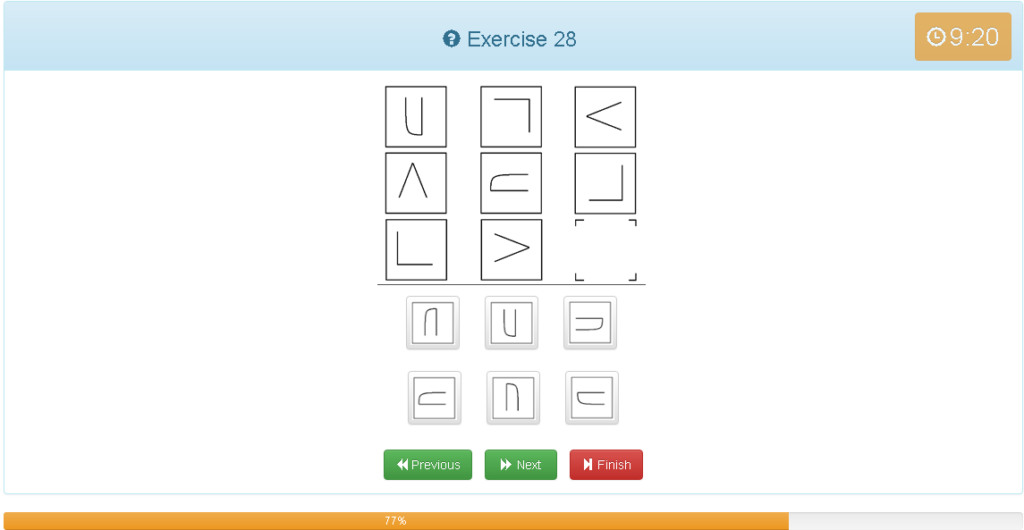
解説

1. 3種類の図形で考える
2. 左から斜めで見ると時計回りで90度回転している

答え

Exercise 29

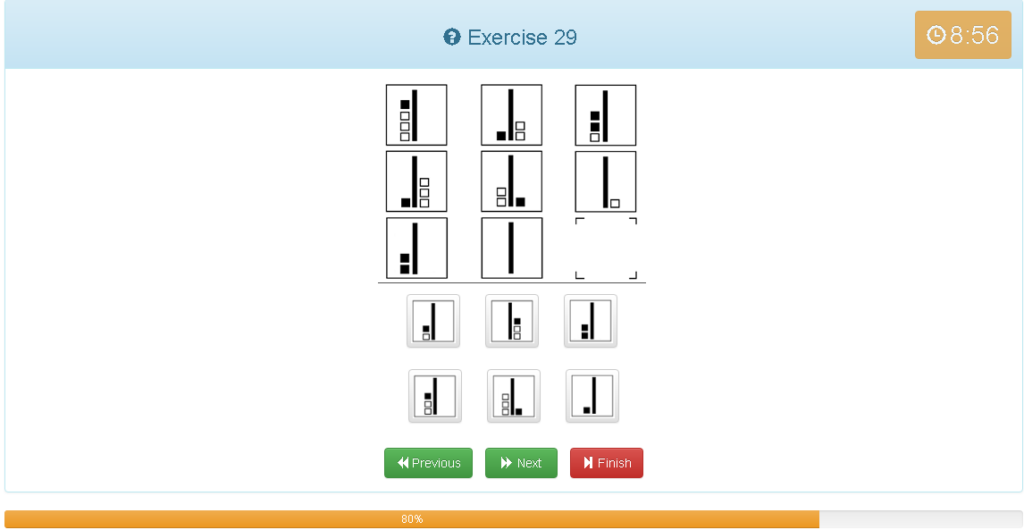
解説

1. 縦横どちらでもグルーピングできる
2. 中心線の左側にあるのが＋、右にあるのが－で考える
3. 例で上段横で考えると、■１＋■１＝■２　□３＋（－□２）＝□１　よってプラス側に■２と□１となる

答え

Exercise 30

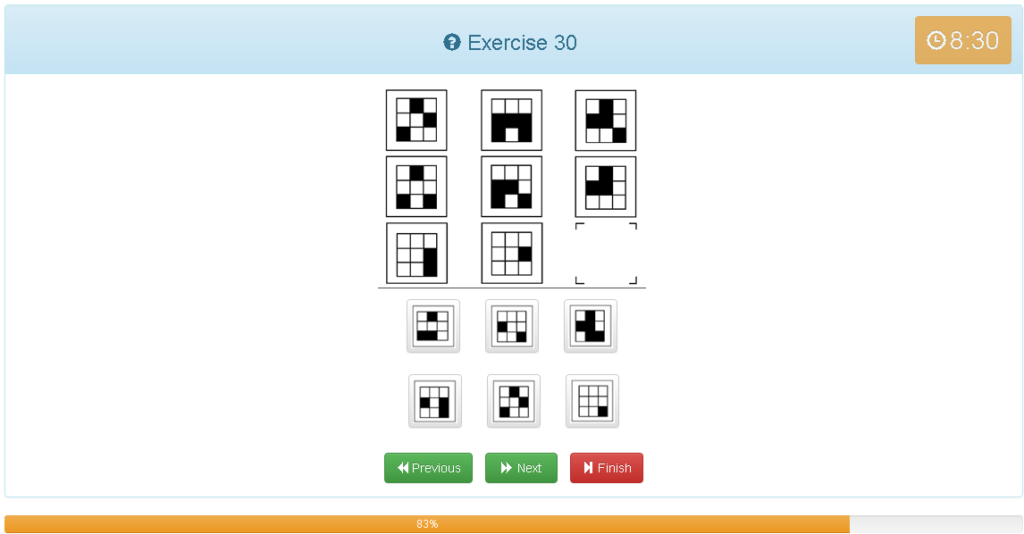
解説

1. 縦横どちらでもグルーピングできる
2. 白＋白＝白
3. 黒＋黒＝白
4. 白＋黒＝黒
5. 1つ目のマス＋2つ目のマス

答え

Exercise 31

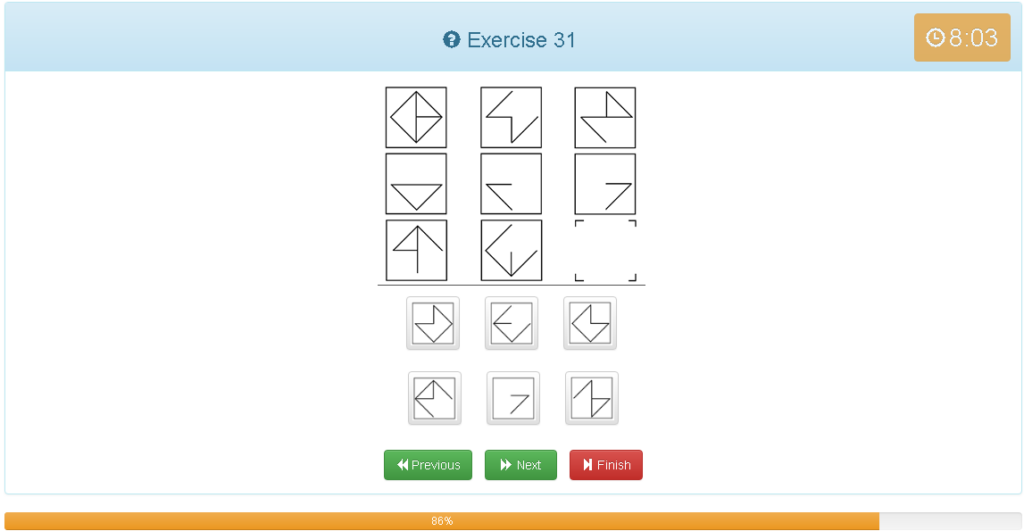
解説

1. 縦横どちらでもグルーピングできる
2. 1つ目の図形に2つ目の図形を足す。
3. 重複した線は消す。
4. この場合横で見るより、縦で見た方が図形が複雑ではないのでわかりやすいと思います。

答え

Exercise 32

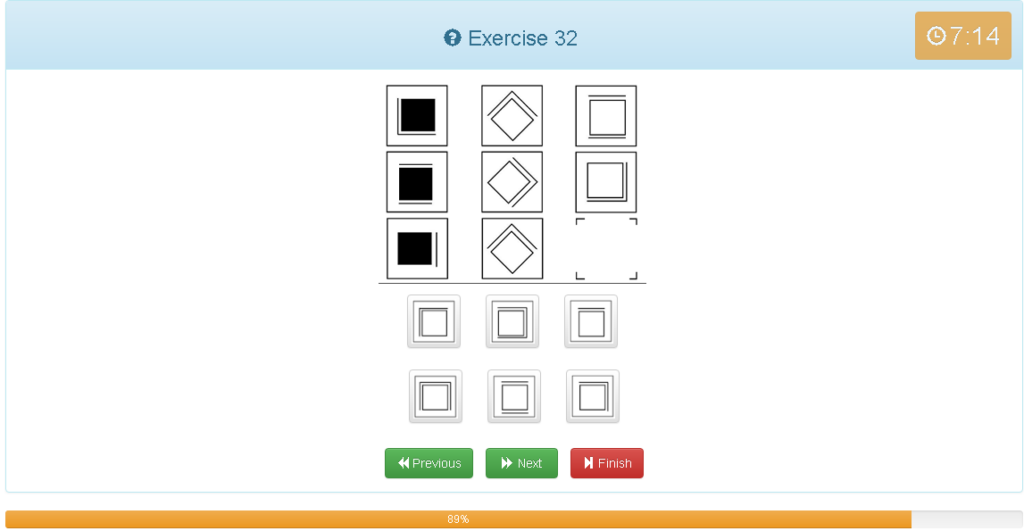
解説

1. 横でグルーピング
2. 回答は□のみなので周りの線のみを考える
3. 2つ目の図形を反時計回りに45度回転させる
4. 重なった線を消す。

答え

Exercise 33

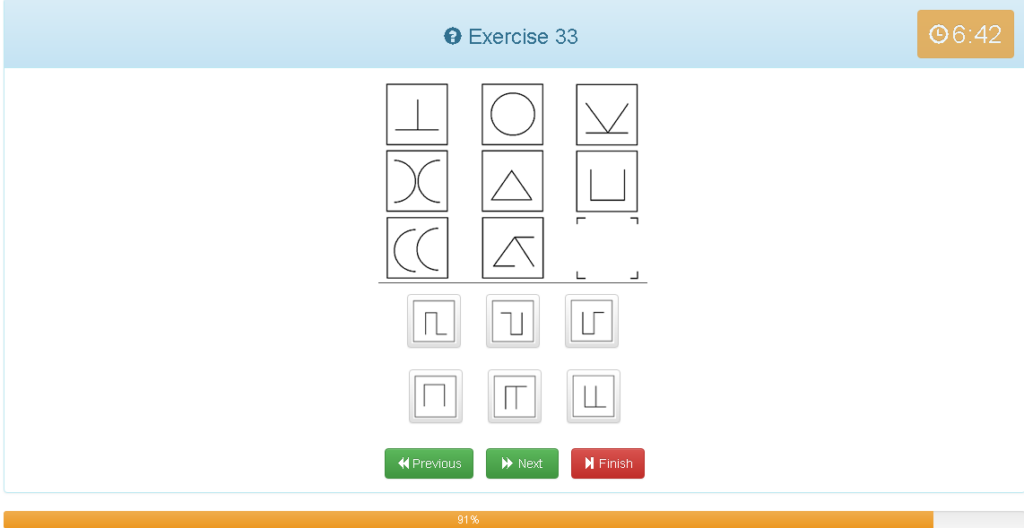
解説

1. 〇・△・コの3種類で考える
2. 〇と△は中心で縦に割り、180度回転と180度反転（裏返し）になっているのが分かる
3. 同じように中心で割り180度回転させれば答えとなる

答え

Exercise 34

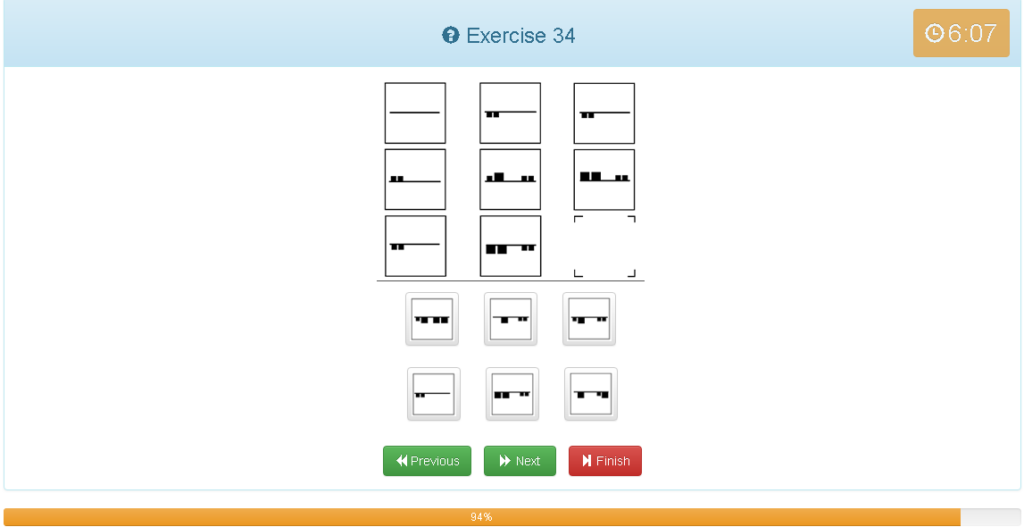
解説

1. 横でグルーピング
2. 小さい■＋小さい■＝大きい■
3. 小さい■＋大きい■＝大きい■
4. 大きい■＋大きい■＝大きい■
5. 1つ目の図形＋2つ目の図形＝3枚目の図形となる

答え

Exercise 35

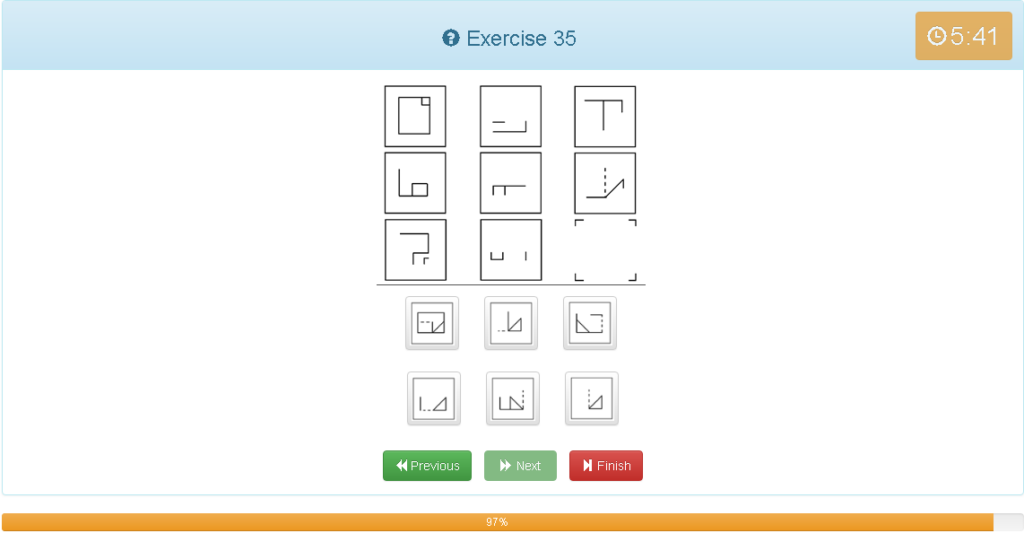
解説

1. 縦でグルーピング
2. 1地番上の図形を反転させる
3. 1つ目の図形＋2つ目の図形
4. 重複した線は消す

答え

さいごに

皆さんいかがでしたか？

説明自体が難しいところもあり、説明が足らないところもあるかもしれませんが、もし詳しく聞きたい方や補足があれば連絡いただければ対応しますので宜しくお願い致します。（良ければ公式LINEからどうぞ。返信は早いです！( ´∀｀ )）

もし、この問題ですらすらと解けるようであればメンサの試験には合格の可能性が高いのではないでしょうか？

とにかくメンサは色々なことが非公開で情報が少ないです。

と言っても、メンサ会員になる最大の難関は【申し込み】なのでまずは【申し込み】を攻略しましょう！

申し込みの簡単な内容をコチラの記事に書いていますのでよろしければ見てください( ´∀｀ )

LINEはじめました！
気になることや疑問があればお応えしますのでお気軽にどうぞ＾＾
個人のLINEではなく、公式アカウントなので安心してください♪